p-进制MRA与GMRA是构造L2(R+)中小波框架的重要工具.L2(R+)中嵌套子空间序列交集为0,并集为L2(R+)是其构成p-进制MRA与GMRA的基本要求.本文研究单个生成元Walsh p-进制平移不变子空间伸缩的交与并,证明了:对任意单个生成元Walsh p-进制平移不变子空间,其p-进制伸缩的交是0;若生成元φ为Walsh p-细分函数,则其p-进制伸缩的并是L2(R+)中一个Walsh p-进制约化子空间.特别地,其伸缩构成L2(R+)中p-进制GMRA当且仅当∪j∈Zpjsupp(Fφ)=R+,其中F为定义在L2(R+)上的Walsh p-进制傅里叶变换.值得注意的是:形式上,我们的结果类似于通常L2(R)的情形,然而其证明不是平凡的.这是因为定义在R+上的p-进制加法“⊕”不同于定义在R上的通常加法“+”.
本文通过经典的可导映射,运用矩阵分块的方法,证明了因子vonNeumann代数A上的每一个非线性混合Lie三重可导映射都是可加的*-导子.
本文考虑带加性噪声的非自治分数阶随机波动方程在无界区域Rn上的渐近行为.首先将随机偏微分方程转化为随机方程,其解产生一个随机动力系统,然后运用分解技术建立该系统的渐近紧性,最后证明随机吸引子的存在性.
本文讨论了2类具体的主理想整环上的拟循环模,研究了A-宽有限的向量空间,刻画了该类向量空间的结构,阐述了A-宽有限的向量空间的A-不变子空间构成的偏序集必满足极小条件,并给出了带有线性变换的向量空间作为F[λ]-模构成拟循环模的一个充要条件.
设λ1,λ2,λ3,λ4为不全为负的非零实数,λ1/λ2是无理数和代数数.V是具有良好间隔的序列,δ>0.本文证明了:对于任意ε>0及v∈V,v≤X,使得不等式|λ1p12+λ2p22+λ3p33+λ4p43-v|<v-δ无素数解p1,p2,p3,p4的v的个数不超过O(X7/8+2δ+ε).这改进了之前的结果.
本文具体计算了系数在超Schrödinger代数J(1/1)的平凡模和有限维不可约模中的第一阶上同调群与第二阶上同调群,并给出了系数在通用包络代数U(J(1/1))中J(1/1)的第一阶与第二阶上同调群的维数是无限维的.
设H4是Sweedler4维Hopf代数.本文根据Rota-Baxter算子的定义和性质,建立H4的权为λ的Rota-Baxter算子在选定基下的矩阵元素满足的二次方程组.通过求解权λ=0时的二次齐次方程组和权λ=1时的二次非齐次方程组,给出了Rota-Baxter算子相应的矩阵形式.
本文对带相依终止事件的复发事件数据提出了一个联合建模分析方法,用一个带脆弱变量的可加可乘比率模型来刻画复发事件过程,还用带脆弱变量的Cox风险率模型来刻画终止事件过程,而且这两个过程的相依性由脆弱变量来刻画.我们利用估计方程的方法,对模型参数进行了估计,给出了所得估计的渐近性质.同时,通过数值模拟分析验证了估计的渐近性质.最后,利用该方法分析了弗吉尼亚大学慢性心脏病病人医疗诊费数据.
具有较强解释力和灵活性的部分线性可加面板数据模型在各学科领域应用广泛.针对个体内存在相关结构的固定效应部分线性可加面板数据模型,本文在结合幂样条函数和最小二乘虚拟变量(LSDV)法的基础上,利用惩罚二次推断函数(PQIF)法对模型进行估计,在一定的正则条件下,证明了参数估计的渐近正态性和非参数估计的收敛性,MonteCarlo数值模拟显示所述估计方法具有良好的有限样本表现,同时,我们还将估计技术应用于实际数据分析中.
利用值分布理论,研究了一类1阶复微分-差分方程
ω(n)(z)2 +[αω(z + c) - βω(z)]2=1
和复微分-差分方程组
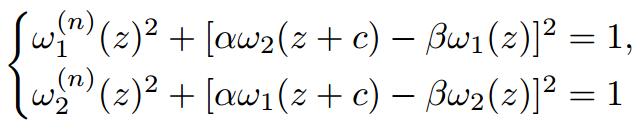
是否存在有限级整函数解的问题.本文推广并改进了高凌云和刘凯等人的结果.
本文研究了广义两分量Dullin-Gottwald-Holm(GDGH2)浅水波系统及其推广形式的一类自相似解.首先通过构造Emden方程,分析了解的全局存在性,以及在一定条件下解的爆破现象;其次利用扰动方法和特征线法,构造了两种形式的精确解.
设A是阿贝尔范畴,X是A的子范畴.Sather-Wagstaff,Sharif和White引入了Gorenstein子范畴的概念,记为G(X).我们用PP(相应地,P)代表纯投射R-模类(相应地,投射R-模类).本文给出了一类满足条件“G(P)⊆G(PP)”的环,由此给出了当W是X的子范畴时,G(W)是否包含在G(X)中的一个否定回答.进一步,刻画了包含关系G(P)⊆G(PP)和G(PP)⊆G(P)何时成立.
本文在K条件下,研究了所给标量泛函的连续性和拟凸性,并利用该标量泛函,将集值优化问题转化为均衡问题,进而研究了含约束的集值优化问题弱充分解的存在性和拟集值优化问题强逼近解映射的上半连续性与下半连续性.与最近的文献相比,我们的方法是新的,条件和结论也更具一般性.
研究了导数的对数属于解析Morrey空间的单叶函数,并建立了解析Morrey域的若干新刻画.