This paper is devoted to the investigation of asymptotic behavior of stochastic Boussinesq equations influenced by random exterior forced white noises both in the velocity and in the temperature fields. It is showed that the stochastic Boussinesq equations can be solved path-wise and the unique solution generates a random dynamical system. Then the existence of a random attractor for the generated random dynamical system is established.

In this paper, the stabilized finite volume method is considered for the R^d,d=2, 3 Stokes equations approximated by the lower order finite element pairs (P₁-P₀ and P₁-P₁), which do not satisfy the so-called inf-sup condition. This method applies the local pressure projection to stabilize the lower order finite element. The convergence analysis also shows an important superclose result O(h²) between the conforming mixed finite element solution and the finite volume solution using the same finite element pair for the incompressible flow. Based on the relationship between the finite element method and finite volume method, optimal estimate and superconvergenc result are obtained. Moreover, the stabilized finite volume method has a convergence rate of the same order as that of the usual stabilized finite element method of the stationary Stokes equations with additional regular assumption on the body force f ∈H¹.

A vertex coloring of a graph G is called r-acyclic if it is a proper vertex coloring such that every cycle C receives at least min{|C|, r} colors. The r-acyclic chromatic number of G is the least number of colors in an r-acyclic coloring of G. We prove that for any number r ≥ 4, the r-acyclic chromatic number of any graph G with maximum degree Δ and with girth at least 2(r ? 1)Δ is at most 6(r ? 1)Δ.

Let G be a finite group, cd(G) be the set of all complex irreducible character degrees of G. In this paper, we investigate the finite solvable groups with irreducible character degrees of arithmetic number, and obtain two results: If cd(G) = {1,1 + d,1 + 2d, ...,1 + kd}, then k ≤ 2 or cd(G) = {1, 2, 3, 4}; if cd(G) = {1, a, a + d, a + 2d, ..., a + kd}, |cd(G)| ≥ 4, (a, d) = 1, then cd(G) = {1, 2, 2^e + 1, 2^e+1}, and present the group structure of case d > 1.

We generalize the oblique principles to the more general g-frames in Hilbert spaces. We give the equivalent condition for a g-frame {Λ_j: j ∈ J} to be an oblique dual g-frame of {Γ_j: j ∈J}. We also give the sufficient condition for a pair of oblique dual g-frames to be symmetric. At the end of this paper we construct several pairs of oblique dual g-frames under different conditions.

By using a Type-function of Sun, the growth of the Laplace-Stieltjes transform convergent in the whole complex plane are obtained, which cover and extend some results of Dirichlet series.

We investigate the question that an entire function and its k-th derivative share some functions by utilizing Nevanlinna theory and Wiman-Valiron theory. We obtain some uniqueness theorems which are closely related to the Brück's conjecture in this direction.

The aim of this paper is to investigate the following parabolic system

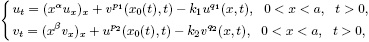
under homogeneous Dirichlet boundary condition, where x₀(t):R⁺→(0,a) is Hölder continuous, and the constants 0≤α, β <1, p₁,p₂,q₁,q₂,k₁,k₂>0. Under appropriate hypotheses, we first prove the local existence of classical solution by a regularization method. Then we discuss the global existence and blow-up of positive solutions by using a comparison principle. Finally, we give the precise blow-up estimates and the uniform blow-up profiles.

In this paper, by using the embedding model of joint tree introduced by Yanpei Liu, we obtain a recurrence relation about the genus distribution of closedend double-ladders on orientable surfaces, and compute the number of embeddings of closed-end multi-ladders on the projective plane.

By introducing Γ-function and ζ-function, and using the way of weight function and the method of real analysis, a Hilbert-type integral inequality with the kernel of hyperbolic cosecant function is given. The equivalent form is considered and their constant factor are proved being the best possible. By taking the special parameter values, some meaningful results are obtained.

K-frames are the generalizations of frames. In this paper, we introduce the definition of a tight K-frame in a Hilbert space, then we give a characterization for tight K-frames by the synthesis operator and the operator K. By means of the operator K, we also obtain a necessary and sufficient condition for tight K-frames to be tight frames. In the end we make a discussion on the construction for tight K-frame and the correlations between two tight K-frames and the involved operator K.

We prove some sharp Hardy inequalities on half spaces for the sublaplacian in Heisenberg group. As a plication, we obtain some sharp Rellich type inequalities for the same operator.

We consider the following semilinear elliptic equation ?Δu-μ(u/|x|² = f(x, u) with the Dirichlet boundary value, and under suitable assumptions on the nonlinear term f. Some existence results of solutions are given via the variational method.

We discuss Voronovskaya-type formulas and saturation of convergence for ω, q-Bernstein polynomials. We give explicit formulas of Voronovskaya-type for ω, q- Bernstein polynomials for 0 < q < 1, 0 ≤ ω ≤ 1. If 0 < q < 1, we show that the rate of convergence for ω, q-Bernstein polynomials is o(qⁿ) if and only if {f(1-q^k-1)-f(1-q^k)}/{(1-q^k-1)-(1-q^k)}=f'(1-q^k), k = 1, 2, .... We also prove that if f is convex on [0, 1] or analytic on (?ε,1+ε) for some ε > 0, then the rate of convergence for ω, q-Bernstein polynomials is o(qn) if and only if f is linear.

We consider the Goursat problem for first-order quasilinear hyperbolic systems. Under the assumptions that the system is weakly linearly degenerate and the boundary conditions on the characteristics are small and decaying, we obtain the existence of global C¹ solutions and give a pointwise estimate to classical solutions. As an important example, we apply this result to the equation for timelike extremal surface in Minkowski space.

Let X be a smooth projective variety of dimension n(n≥3) and ε an ample vector bundle with rank r=n-k(k≥1) over X. We denote Λ(ε,K_X)=max{(-K_X-c₁(ε))·C|R=R+[C]∈Ω, and l(R)=-K_X·C}, where K_X is the canonical bundle of X, c₁(ε) means the first Chern class of ε, Ω denotes the set of extremal rays R such that (K_X+c₁(ε))·C≤0, R₊ is the set of positive real number, and l(R) is the length of R. The classification of (X, ε) will ba given when Λ(ε,K_X)≥k-1.

We establish some sharp maximal function inequalities for the Toeplitz type operator related to certain singular integral operators satisfying a variant of Hörmander's condition. As an application, we obtain the boundedness of the operator on Lebesgue, Morrey and Triebel-Lizorkin spaces.

Let M_Ω,α and T_Ω,α be the fractional maximal and integral operators with rough kernels, where 0<α<n. In this paper, we shall study the continuity properties of M_Ω,α and T_Ω,α on the weighted Morrey spaces L^p,κ(w). The boundedness of their commutators with BMO functions is also obtained.

We consider the class of Moran sets satisfying the conditions c_*>0 and s_*=s_*∈(0, 1). We obtain that two Moran fractals in the class are quasi-Lipschitz equivalent if and only if they have the same Hausdorff dimension.

In this note, we adapt the scaling method and give the blow-up estimates for a system of heat equations coupled boundary flux.

Special functions that satisfy linear differential equations with polynomial coefficients appear ubiquitously in combinatorics and mathematical physics. Such kind of special functions are called D-finite functions by Stanley. In the early 1980's, many combinatorists, such as Gessel, Stanley, Zeilberger etc., conjectured that the diagonal of rational power series in several variables is D-finite. Gessel and Zeilberger proved this conjecture in their papers, respectively. Later, Lipshitz pointed out that their proofs are not complete and he gave a proof by basing on a different idea. Zeilberger completed his proof with the theory of holonomic D-modules. In this note, we follow the spirit of Gessel's proof strategy and fix the gap in his proof in the case of bivariate rational formal power series. The key ingredients we used are some basic properties of the diagonal operation.

Given a graph G=(V,E), S⊆V, the minimal number of S whose removal eliminates all the cycles in G is called the decycling number, denoted as ∇(G). The problem of deternimating the decycling number of a graph is NP-complete. Bau and Beineke proposed the following question: which cubic graphs of order 2n have decycling number [n+1/2]? In this paper we proved that generalized Petersen graph P(n, k) is such a class of graphs. Based on this result, we proved that P(n, k) is upper-embeddable which generalized a result of Ren.

We made some further research on the coarse embeddability between l_p spaces and l₂ and we proved that a metric space X can be coarsely embedded into l₂ if and only if there exists some p₀>0 such that X can be coarsely embedded into l_p, 2<p≤p₀} uniformly. This gave an equivalent condition for the coarse embeddability of metric spaces into l₂.

Let 1<r<∞, B_j and φ_j (j=1,...,m) are suitable functions. We say a kernel K satisfies a variant of the classical L^r-Hörmander's condition, if there exist constants c^r>0 and C^r>0, such that for any y∈Rⁿ and R>c^r|y|,

. In this paper, the authors establish the weighted norm inequalities for singular integral operators with kernel satisfying the above variant of the classical L^r-Hörmander's condition.

We investigate the boundedness and compactness of Toeplitz operators with L¹ symbols on weighted Bergman spaces of the unit ball A_α^p(B_n, dV_α) (1<p<∞). We describe the boundedness and compactness of Toeplitz operators with L¹ symbols on A_α^p(B_n, dV_α) equivalently by using the Berezin transform of the Toeplitz operators, and promote the conclusion given by Agbor about the boundedness and compactness of Toeplitz operators with L¹ symbols on Bergman space of the unit disk L_a²(D).

We deal with the existence of weak and strong solutions for Oseen equations in the case that the divergence of convective vector is nonzero. Using Lax-Milgram Theorem, we first prove the existence of weak solution in H¹(Ω), and then on the basis of this result, we use methods of iterative and dual principle to prove the existence of weak and strong solutions in generic Sobolev spaces and obtain corresponding estimates for these solutions.

Let G be finite group such that M(G)=M(G₂(3ⁿ)), where n≥1. Then G has a normal subgroup isomorphic to G₂(3ⁿ). Especially, if |G|=|G₂(3ⁿ)|, then G≌G₂(3ⁿ).

For λ<n and λ=0, Rubin introduced the concept of the λ-intersection body IB_λ(K) of an origin-symmetric star body K in Rⁿ. In this paper, we consider Busemann-Petty's problem of whether IB_λ(K)⊆IB_λ(L) implies vol_n(K)≤vol_n(L) (or vol_n(K)≥vol_n(L)). We proved that Busemann-Petty's problem of λ-intersection body in Rⁿ has a positive answer if and only if any origin-symmetric star body in Rⁿ is a λ-intersection body. Our results generalize the specific affirmative answer of classic intersection bodies to Busemann-Petty problem.

In this paper, the concepts of the i th L_p-mixed affine surface area and L_p-polar curvature images are introduced, some new inequalities connecting these new notions with L_p-centroid bodies and p-Blaschke bodies are established. Moreover, a Blaschke-Santaló type inequality for L_p-mixed affine surface area is established. Our results also imply a generalization of the class dual Urysohn inequalities.

We are concerned with the existence of positive solutions of the nonlinear Neumann problem (p(t)u')'+q(t)u=f(t, u), t ∈ (0, 1), u'(0)=u'(1)=0, where p, q ∈ C[0, 1] with p > 0, 0 < q < b^* in [0, 1], b^* is the first eigenvalue of the Robin problem (p(t)u')'+bu=0, u'(0)=0, u(1)=0. By applying the topological degree theory and global bifurcation techniques, we establish the existence results of positive solutions for above problem.

Representations of abstract effect algebras was introduced in the literature [Sci. Sin. Math., 2011, 41(3): 279-286], some examples of representable effect algebras and unrepresentable effect algebras were given there. However, a general criterion about the representations of effect algebras was not obtained. Based on the idea of the GNS structure of an abstract C^*-algebra, we guess that abstract effect algebras admitting much enough states should be representable. Thus, the existence of states and the representations of state spaces seem to be important in the representation theory and the classification problem of abstract effect algebras. This paper is devoted to discussing the existence of states and valuations of effect algebras. General forms of states and state spaces of some typical effect algebras are obtained. Especially, the existence theorem of states of representable effect algebras is proved and nonempty convex subsets of state space and valuation space of an effect algebra are given, respectively.

We characterize the bounded ness and compact ness of the Toeplitz operators on the harmonic Dirichle space; discuss the algebraic properties of the Toeplitz operators; and obtain the short exact sequences with respect to the Toeplitz algebra and the Hankel algebra. We also compute the Fredholm index of Fredholm operator in the Toeplitz algebra and the Hankel algebra, and obtain the K₀ and K₁ groups of the Toeplitz algebra and the Hankel algebra.

Let kG be a group algebra, and D(kG) the quantum double of kG. We first prove that the structure of representation ring of D(kG) can be described in terms of the representation ring of centralizer subgroups of representatives of conjugate classes of G. As an application, we then describe the structure of representation ring of D(kG_n), where k is a field of characteristic 2, n is odd, and D_n is a dihedral group of order 2n.

It is mainly proved: let k ≥ 2 be a positive integer, M a positive number, let c (≠0) be a finite value, and let F be a family of meromorphic functions in a domain D, all of whose zeros are of multiplicity k at least. If, for each function f ∈ F, f(z)=0⇔f^(k)(z)=0, f^(k)(z)=c⇒|f^(k+1)(z)| ≤ M, then F is normal in D. And c ≠ 0 is necessary.

In this paper, for the approximation in L_p-norm, we determine the weakly asymptotic order for the p-average errors of a kind of quasi-Hermite interpolation sequence on the 1-fold integrated Wiener space. By the result it is known that in the sense of Information-Based Complexity, if permissible information functions are Hermite data, then the p-average errors of this interpolation sequence are weakly equivalent to the corresponding minimal p-average radius of nonadaptive information.

An r-graph is a loopless undirected graph in which no two vertices are joined by more than r edges. An r-complete graph on m+1 vertices, denoted by K_m+1^(r), is an r-graph on m+1 vertices in which each pair of vertices is joined by exactly r edges. A non-increasing sequence π=(d₁, d₂,..., d_n) of nonnegative integers is said to be r-graphic if it is the degree sequence of some r-graph on n vertices. An r-graphic sequence π is said to be potentially (resp. forcibly) K_m+1^(r)-graphic if π has a realization containing K_m+1^(r) as a subgraph (resp. every realization of π contains K_m+1^(r) as a subgraph). Let σ(K_m+1^(r), n) (resp. τ (K_m+1^(r), n)) denote the smallest even integer t such that each r-graphic sequence π=(d₁,d₂,..., d_n) with ∑_i=1ⁿd_i ≥ t is potentially (resp. forcibly) K_m+1^(r)-graphic. Clearly, σ(K_m+1^(r), n) is an extension from 1-graph to r-graph of a conjecture due to Erdös et al and τ (K_m+1^(r), n) is an extension from 1-graph to r-graph of the classical Turán's theorem. In this paper, we give two simple sufficient conditions for an r-graphic sequence to be potentially K_m+1^(r)-graphic, which imply two main results due to Yin and Li (Discrete Math., 2005, 301: 218-227) and the value of σ(K_m+1^(r), n) for n ≥ max{m²+3m+1-[m²+m/r], 2m+1+[m/r]}. Moreover, we also determine the value of τ(K_m+1^(r), n) for n ≥ m+1.

In this paper, the authors characterize the boundedness and compactness of the integral-type operator P_g from mixed norm spaces H(p, q, φ) to Zygmund-type spaces on the unit ball and some necessary and sufficient conditions of the integral-type operator P_g to be bounded and compact are obtained.

In this paper, using a scalarization technique, we provide sufficient conditions for the upper/lower semicontinuity of the solution mappings to parametric setvalued weak vector equilibrium problems without monotonicity and C-concavity in linear metric spaces. These results improve the recent ones in the literature. Some examples are given for illustration of our results.

The skew energy E_S(D) of a digraph D is defined as the energy of its skewadjacency matrix. In this paper, employing many operations of digraphs, we construct several classes of digraphs, each one of which satisfies its skew energy is the same as the energy of its underlying graph. This work partly answers a problem proposed by Adiga et al. [The skew energy of a digraph, Linear Algebra Appl., 2010, 432: 1825-1835].

In this paper, the elementary symmetric functions μ₀, μ₁,..., μ_n and the intrinsic volumes V₀,V₁,..., V_n are investigated. We show that the elementary symmetric function basis {μ₀, μ₁,..., μ_n} and the intrinsic volume basis {V₀,V₁,..., V_n} defined on Lⁿ (also the quermassintegral basis {W₀,W₁,..., W_n}) are equivalent.