在2002,2007的文章中,蔡天新等人介绍了一系列关于二项式系数模平方数的同余式.本文将这些同余式进行改进并推广到了模为立方数的情形,得到了许多新的同余式.如对任意正整数k和正奇数n,当e=2,3,4和6时,Πd|n(└d/e┘kd-1)μ(n/d)模n3的同余式,以及下面这类有趣的同余式
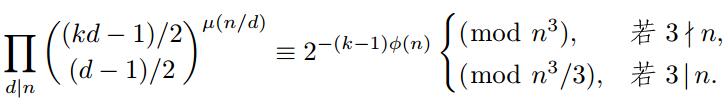
本文研究了Hilbert C*-模上可共轭算子的并联和,推广了矩阵和Hilbert空间上有界线性算子的一些相关结果.通过举例说明:存在一个Hilbert C*-模H,以及H上的两个可共轭的正算子A和B,使得算子方程A1/2=(A+B)1/2X,X∈L(H)无解,其中L(H)为H上的可共轭算子全体.
我们定义纯奇点范畴Dpsgb(R)为有界纯导出范畴Dpurb(R)与纯投射模构成的有界同伦范畴Kb(PP)的Verdier商,得到了纯奇点范畴Dpsgb(R)三角等价于相对纯投射模的Gorenstein范畴的稳定范畴G(PP)的一个充分必要条件.同时,还给出三角等价Dpsgb(R)≈Dpsgb(S)的充分条件,这里R和S都是环.
利用有界(消失)平均振荡函数的性质,本文刻画了一类广义Fock空间上的Hankel算子的有界性(紧性),同时,还刻画了换位子[Mf,P]的有界性和紧性,其中P是一个Toeplitz投影算子,而Mf表示符号为f的乘子.最后,应用Berezin变换来研究了BMO空间和VMO空间的几何性质.
作为Cantor型集的推广,文志英和吴军引入了齐次完全集的概念,并基于齐次完全集的基本区间的长度以及基本区间之间的间隔的长度,得到了齐次完全集的Hausdorff维数.本文研究齐次完全集的拟对称极小性,证明在某些条件下Hausdorff维数为1的齐次完全集是1维拟对称极小的.
受Peng-中心极限定理的启发,本文主要应用G-正态分布的概念,放宽Peng-中心极限定理的条件,在次线性期望下得到形式更为一般的中心极限定理.首先,将均值条件E[Xn]=E[Xn]=0放宽为|E[Xn]|+|E[Xn]|=O(1/n);其次,应用随机变量截断的方法,放宽随机变量的2阶矩与2+δ阶矩条件;最后,将该定理的Peng-独立性条件进行放宽,得到卷积独立随机变量的中心极限定理.
本文利用Brown运动在Hölder范数下的大偏差和小偏差,得到了Brown运动增量在Hölder范数下的局部泛函Chung重对数律.
利用无界Hamilton算子导出的二次算子族,本文研究了一类无界Hamilton算子根向量组的Schauder基性质.首先,建立了无界Hamilton算子的根向量与相应的二次算子族的根向量之间的关系.其次,借助二次算子族谱的相关性质,刻画了无界Hamilton算子的本征值分布以及本征值的代数指标,并得到了无界Hamilton算子的根向量组是某个Hilbert空间的一个块状Schauder基的充要条件.最后,将所得结果应用于矩形薄板弯曲问题.
该文给出了广义映射Schrödinger-Virasoro代数的所有二上同调群,并且给出了这类李代数的所有泛中心扩张.
在《数学学报》2013年第56卷第4期中,“Suzuki-Ree群的自同构群的一个新刻画”一文证明了Aut(2F4(q)),q=2f和Aut(2G2(q)),q=3f,可由其阶分量刻画,其中f=3s,s为正整数.本文证明了Aut(2B2(q)),q=2f和Aut(2G2(q)),q=3f,也可由其阶分量刻画,其中f为奇素数.结合二者得到结论:Suzuki-Ree单群的所有的素图不连通的自同构群皆可由其阶分量刻画.
设R⊂A是环的Frobenius扩张,其中A是右凝聚环,M是任意左A-模.首先证明了AM是Gorenstein平坦模当且仅当M作为左R-模也是Gorenstein平坦模.其次,证明了Nakayama和Tsuzuku关于平坦维数沿着Frobenius扩张的传递性定理的“Gorenstein版本”:若AM具有有限Gorenstein平坦维数,则GfdA(M)=GfdR(M).此外,证明了若R⊂S是可分Frobenius扩张,则任意A-模(不一定具有有限Gorenstein平坦维数),其Gorenstein平坦维数沿着该环扩张是不变的.
本文借助集合极限的性质和弱f-性假设证明了含参广义集值强向量平衡问题解集映射的下半连续性,其方法不同于最近文献(Zhao,2016和Meng,2018).此外,建立了含参广义集值强向量平衡问题解集连通性的充分条件,并举例验证了所得结果的正确性.本文得结果推广和改进了已有文献(Gong,2008,Xu,2009,Chen,2010,Xu,2013和Zhao,2013)中相应结果.
本文针对时空分数阶非线性薛定谔方程,提出了应用Padé,近似逼近Mittag-Leffler函数的指数时间差分格式,讨论了提高格式计算效率的方法.本文在具有各种参数的时空分数阶非线性薛定谔方程上进行了数值实验,实验结果说明了所提出方法的准确性、有效性和可靠性.