尹建华
一个r-图是一个无环的无向图,其中任何两个顶点之间至多被r条边连接.一个m+1个顶点的r-完全图, 记为Km+1(r),是一个m+1个顶点的r-图, 其中任何两个顶点之间恰好被r条边连接.一个非增的非负整数序列π=(d1, d2,..., dn)称为是r-可图的如果它是某个n个顶点的r-图的度序列.一个r-可图序列π称为是蕴含(强迫)Km+1(r)-可图的如果π有一个实现包含Km+1(r)作为子图(π的每一个实现包含Km+1(r)作为子图). 设σ(Km+1(r),n)τ (Km+1(r), n))表示最小的偶整数t,使得每一个r-可图序列π=(d1, d2,..., dn)具有∑i=1ndi ≥ t是蕴含(强迫) Km+1(r)-可图的.易见,σ(Km+1(r),n)是Erdös等人的一个猜想从1-图到r-图的扩充且τ (Km+1(r), n))是经典Turán定理从1-图到r-图的扩充.本文给出了蕴含Km+1(r)的r-可图序列的两个简单充分条件.此两个条件包含了Yin和Li在[Discrete Math., 2005, 301:218-227]中的两个主要结果和当n ≥ max{m2+3m+1-[m2+m/r], 2m+1+[m/r]}时,σ(Km+1(r),n)之值. 此外, 我们还确定了当n≥m+1时,τ (Km+1(r), n))之值.
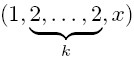 =∑n ≤ xd
=∑n ≤ xd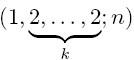 的渐近公式, 这里d
的渐近公式, 这里d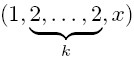 =∑n=ab12…bk21. 然后基于以上结论得到了指数除数函数τk(e)(n)的均值的渐近公式, 并改进了前人的结果.
=∑n=ab12…bk21. 然后基于以上结论得到了指数除数函数τk(e)(n)的均值的渐近公式, 并改进了前人的结果.