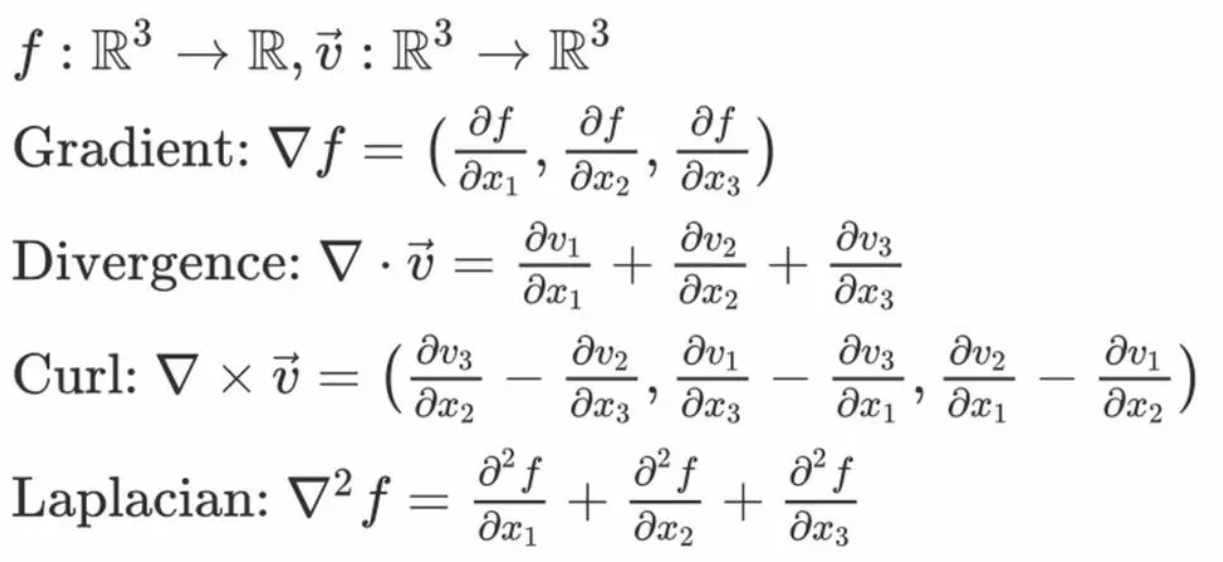动力系统 (dynamical system) 是数学上的一个概念。
在动力系统中存在一个固定的规则,描述了几何空间中的一个点随时间演化情况。例如描述钟摆晃动、管道中水的流动,或者湖中每年春季鱼类的数量,凡此等等的数学模型都是动力系统。
若只是在一系列不连续的时间点考察系统的状态,则这个动力系统为离散动力系统;若时间连续,就得到一个连续动力系统。如果系统以一种连续可微的方式依赖于时间,我们就称它为一个光滑动力系统。
泛函分析是现代数学中的一个重要分支,主要研究的是函数构成的空间,即函数空间。泛函分析的形成与发展得益于对函数空间和函数变换(如傅立叶变换等)性质的研究,以及对微分方程和积分方程的应用。泛函的定义域通常是函数空间中的一个元素,而值域则是实数集或实数集的一个子集。
泛函可以视为从函数空间到数域的映射,其中函数的自变量可以是函数自身或其他函数。泛函的概念不仅扩展了古典分析的基本概念和方法,而且将这些概念和方法几何化,从而形成了一种抽象空间的概念。
代数是研究数、数量、关系、结构与代数方程的数学分支,也是数学中最重要的、基础的分支之一。代数有两种含义:广义的和狭义的。广义的代数是指群、环、域、模、线性空间等,这些结构及研究他们的方法论的总和; 狭义的代数一般专指向量空间上定义了某种满足一些公理化条件的乘法后的这种结构。
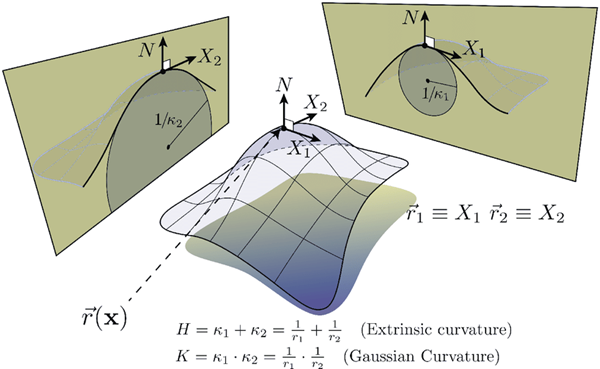
几何是研究空间结构及性质的一门学科。它是数学中最基本的研究内容之一,与分析、代数等等具有同样重要的地位,并且关系极为密切。几何学发展历史悠长,内容丰富。它和代数、分析、数论等等关系极其密切。几何思想是数学中最重要的一类思想。
概率统计是一门研究随机现象的发生规律、规律性和定量化研究的学科。概率统计主要包括两个部分:概率论和数理统计。
概率论是研究随机现象的基本概念、性质、规律及其应用的学科。它主要研究事件发生的可能性大小及其规律性;
数理统计是应用概率论的方法对数据进行分析和处理的学科。它主要研究如何根据已有数据推断出总体的某些特征参数,例如总体的均值、标准差、方差等等。数理统计包括描述统计和推断统计两个方面。
偏微分方程理论研究一个方程(组)是否有满足某些补充条件的解(解的存在性),有多少个解(解的惟一性或自由度),解的各种性质以及求解方法等等,并且还要尽可能地用偏微分方程来解释和预见自然现象以及把它用之于各门科学和工程技术。偏微分方程理论的形成和发展都与物理学和其他自然科学的发展密切相关,并彼此促进和推动。其他数学分支,如分析学、几何学、代数学、拓扑学等理论的发展也都给予偏微分方程以深刻的影响。
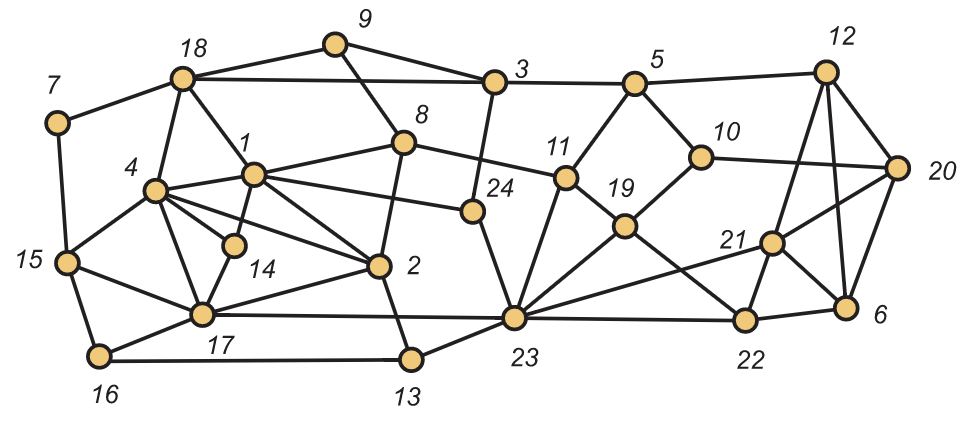
组合图论是一门包含组合计数,组合设计,组合矩阵,组合优化等众多分支的不可以轻视的科学。组合数学和图论的几类经典问题,包括四色问题、七桥问题、哈密顿问题、最短路问题、拉姆赛数问题、斐波那契数列问题等。
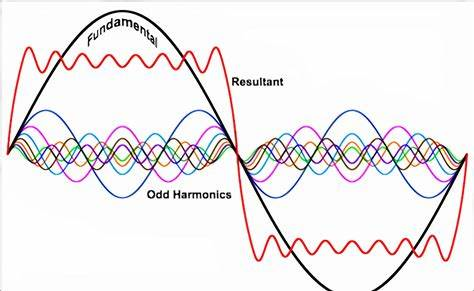
调和分析是现代分析数学的一个核心领域,它的起源可以追溯到物理学中的一个基本问题:如何将一个周期振荡分解为简谐振荡的迭加。调和分析的主要内容包括函数展开成傅立叶级数或傅立叶积分,以及这些问题相关的各种运算。这个领域的数学工具包括傅立叶变换,它在数学、信息处理、量子力学等多个学科中都有广泛的应用。