本文利用三个控制函数给出了半序Menger PM-空间中满足特定条件的广义弱压缩映射的最佳逼近点定理,并给出了最佳逼近点唯一的充分条件.进一步地,还给出了主要结果的一些推论.
本文首先给出了非自治随机动力系统的随机一致指数吸引子的概念及其存在性判据,其次证明了Rn上的带加法噪声和拟周期外力的FitzHugh—Nagumo系统的随机一致指数吸引子的存在性.
本文引入广义中心α-Armendariz环的概念,得到了广义中心α-Armendariz环的基本性质,研究了广义中心α-Armendariz环与其他环之间的一些关系.
本文在Sobolev—Lorentz空间W 2L2,q(R4)的范数约束下得到了一个最佳的二阶次临界型Adams不等式.进一步,当次临界指标逼近最佳常数时,得到了Adams泛函的上、下界的估计.本文主要采用了Lam和Lu[A new approach to sharp Moser—Trudinger and Adams type inequalities:a rearrangement-free argument,J. Diff. Equ.,2013,255(3):298—325]的分割水平集方法.
非等熵气体动力学系统Cauchy问题弱解全局存在性有两个公开问题:一个是包含真空的小初值问题,另一个是任意大初值问题.本文通过引入一个放缩框架证明了上述两个问题的等价性,即对于粘性消失解,其包含真空小初值问题的一致BV估计蕴含着任意大初值问题弱解的全局存在性.该放缩框架对大多数具有物理背景的双曲守恒律系统亦成立.
本文考虑Baskakov算子的一种新的局部化算子,获得了该算子的一些收敛性质.另外,利用概率论中心极限定理,建立了Baskakov算子核的新估计
本文研究如下分数阶Schrödinger—Poisson方程
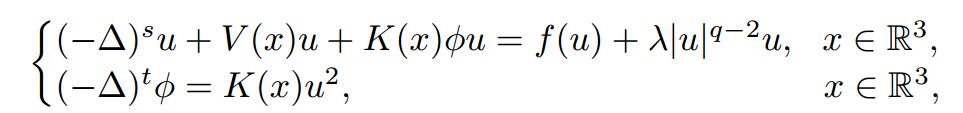
其中s ∈(4/3,1),t ∈(0,1),f是在原点超线性无穷远次临界的连续非线性项,指数q ≥ 2s*=(3-2s)/6.当λ>0充分小时,我们利用变分方法证明上述问题正解的存在性.本文的主要贡献是处理了超临界情形.
本文利用凸刻画系数和正规结构系数,詹姆斯型常数和García-Falset系数之间的关系式,得到了空间上集值非扩张映射存在不动点的一些充分条件,这些结论不仅改进了一些文献中的结果,而且也对一些公开问题给出了解答.
本文主要研究以下形式的Hausdorff算子Hφf(x)=∫Rnφ(u1,...,un)f(u1x1,...,unxn)du1 · · · dun,其中φ是Rn上的缓增分布.当n ≥ 2,0<p<1,若φ是Schwartz函数,我们得到Hφ在Hp(Rn)上有界当且仅当φ=0.进一步,当n ≥ 2,(n+1)/n<p<1,如果φ仅仅是连续函数,并且Hφ有合适定义,那么Hφ在Hp(Rn)上有界当且仅当φ是常数.这些结果都表明Hausdorff算子Hφ在Hp(Rn)上的有界性很复杂.此外,我们将Hφ转化成卷积型算子,得到Hφ在Lebesgue空间上有界的一些新的结果.
本文说明Banach空间上p-fusion框架和p-框架有紧密联系.应用分析算子和合成算子给出p-fusion Bessel序列、p-fusion框架和q-fusion Riesz基的等价描述.
设R是环,R的小finitistic维数定义为fPD (R)=sup{pdRM|M∈FBR}.本文证明了:若R是连通的强Prüfer环,则fPD (R ≤ 1.也证明了若R是强Prüfer环,M∈FBR,且M是Q-挠模,则pdRM ≤ 1.
本文研究如下带有临界增长的分数阶Kirchhoff方程ε2sM(ε2s-3 ∫∫R3×R3·(|u(x)?u(y)|2)/(|x-y|3+2s)dxdy)(-Δ)su+V(x)u=λW(x)f(u)+K(x)|u|2s*-2u,x ∈ R3,其中M是一个连续正的Kirchhoff函数,λ>0是一个参数,3/4<s<1,2s*:=6/(3-2s)是3维的临界指数,并且V(x),W(x)和K(x)都是正位势函数.在Kirchhoff函数M和位势函数的适当假设下,当ε>0充分小和λ足够大时,我们首先证明了上述问题正基态解的存在性.其次,证明了基态解集中在一个由位势函数所刻画的特定集合中.最后,研究了基态解的衰减估计.