我们定义了KS-变换和自然数乘法结构相关的Fourier变换,建立了实数乘法半群[1,∞)={x:x∈R,x ≥ 1}和复半平面Ω={s=σ+it:σ,t∈R,σ ≥ 1/2}之间的由KS-变换诱导的对偶关系,证明了KS-变换是希尔伯特空间L2([1,∞))和哈代空间H2(Ω)之间的等距算子,而且该算子保持了相关的函数空间之间由实数的乘法卷积和复数点点相乘诱导出的代数结构的同构.作为应用,我们给出了黎曼假设成立的有关算子指标的等价命题,从而算子理论为研究黎曼ζ-函数和自然数的乘法结构提供了新思路.
利用小波方法在局部Hölder空间中研究一类反卷积密度函数的点态估计问题.首先,针对超级光滑噪声给出该模型任一估计器的点态风险下界;其次,构造有限求和小波估计器,并证明其在超级光滑噪声条件下达到了最优收敛阶,即该估计器在点态风险下的收敛速度与下界一致.最后,还讨论了这类小波估计器的强收敛性.值得指出的是上述估计都是自适应的.
设AT(Δ)是单位圆盘Δ上所有渐近Teichmüller等价类[[μ]]或[[fμ]]构成的渐近Teichmüller空间.本文证明了对AT(Δ)内的任意渐近极值的fμ,总存在一个[[fμ]]内的渐近极值映射gν,使边界伸缩商h*(μf?g-1(g(z))})≠0.同时也获得了AT(Δ)在基点处的切空间上的类似结果.
本文研究了有穷级亚纯函数的导数及其差分分担值的唯一性问题,主要证明了以下结论:如果f'与Δcf CM分担a,b,∞,则f'≡Δcf.该结论解决了Qi等人在2018年提出的问题.
在[Anomaly cancellation and modularity,Frontiersin Differential Geometry,Partial Differential Equations and Mathematical Physics,2014:87-104,World Sci.Publ.,Hackensack,NJ]中,韩-刘-张给出了一个反常消去公式,推广了Green-Schwarz公式和Schwartz-Witten公式.本文研究了两个推广的韩-刘-张公式和一个奇数维的韩-刘-张公式.通过研究一些示性式的模性质,给出了奇数维新的反常消去公式.
本文研究带形上的近临界随机游动,借助游动常返暂留性判别准则的显式表达,通过带扰动的线性差分系统的解的渐近性理论,以及矩阵的范数性质,在扰动矩阵不同的阶的条件下,给出了游动常返暂留性的判别.
本文借鉴Bressan和Constantin于2007年提出的新特征线法,利用具有强迫项的Dullin-Gottwald-Holm方程的平衡律和一些新的估计,证明了该方程在H1(R)中整体耗散解的存在性.
本文在Hilbert空间上引入了一个新的粘性迭代算法,找到了关于两个逆强单调算子的变分不等式问题的解集与非扩张映射的不动点集的公共元.通过修改的超梯度算法,得到了强收敛定理,也给出了一个数值例子.所得结果改进了许多最新结果.
本文将时齐马氏过程中重要的代数不等式Liggett-Stroock不等式推广到非时齐马氏过程中,建立了非时齐马氏过程的转移半群与Liggett-Stroock不等式之间的关系.
本文首先证明了一个新的从Cn到PN(C)的亚纯映射第二基本定理,其中涉及到带有不同权重的截断型计算函数;其次利用这个新的第二基本定理,考虑了退化的亚纯映射在分担处于一般位置的移动超平面下的唯一性问题,并在较弱的条件下获得了一个唯一性结果,改进了已有的一些经典结果.
本文讨论了多复变中单位球上正规权Zygmund空间Zμ(B)的一些性质.首先给出了Zμ(B)函数的一种积分表示,接着证明了Zμ(B)是正规权Bergman空间Aν1(B)的对偶空间,其对偶对按如下形式给出:
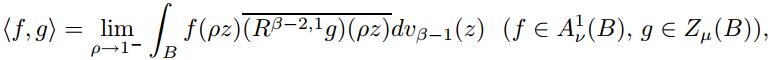
其中ν(ρ)=(1-ρ2)β+1μ-1(ρ)(0 ≤ ρ<1)并且β>max{0,b-1}.最后作为积分表示和对偶的一个应用,作者给出了Zμ(B)中每个函数的一个原子分解.
本文引入了一个广义的约当-冯诺依曼型常数,并研究了它的相关性质,同时还利用广义的约当-冯诺依曼型常数,弱正交系数μ(X)和Domínguez-Benavides系数R(1,X),对Banach空间中的弱收敛序列系数WCS(X)进行了估计,从而得到了空间具有正规结构的一些充分条件.这些结论严格推广了最近一些文献中的结果.