设G是有限秩的幂零群，1=ζ0G < ζ1G < … < ζcG=G是G的上中心列，End（ζiG/ζi-1G）是Abel群ζiG/ζi-1G的自同态环（1 ≤ i ≤ c），End（ζiG/ζi-1G）可以自然地作成一个 Lie 环.α1，α2，…，αn是G的n个自同构，把它们在ζiG/ζi-1G上的诱导自同构分别记为α1i，α2i，…，αni （1 ≤ i ≤ c）.如果由α1i，α2i，…，αni生成的 Lie环End（ζiG/ζi-1G）的 Lie 子环都是完全可解的，那么 α1，α2，…，αn生成的AutG的子群具有良好的幂零性质.考虑G的下中心列，可以得到对偶的结果.
当p ≥ 5，n ≥ 0 时，（i1i0）*（hn）∈ExtA1，pnq（H*K，Zp） 在Adams 谱序列中是永久循环，并且收敛到 πpnq-1K 中的非零元.本文在此基础上，考虑了涉及第三希腊字母类乘积元素的收敛性，并且扩大了球面稳定同伦群中非平凡元素滤子s+1的取值范围，即当p+1 < s+1 < 2p时，
shn∈ ExtAs+1，t（Zp，Zp） 在Adams谱序列中是永久循环，并且收敛到πt-s-1S中的非零元γsξn，其中p ≥ 7，n ≥ 3 t=pnq+sp2q+（s-1）pq+（s-2）q+s-3，q=2（p-1）.
本文给出了A进方体满足嵌套性质的一个充分条件，得到了A进方体的一个覆盖定理，探讨了A进方体与相关于扩张矩阵A的Christ-二进方体的关系.
本文研究了短区间的并集中整数及其m次幂的差的均值分布问题，给出了渐近公式.具体来说，设p是奇素数，1 ≤ H ≤ p，实数δ满足0 < δ ≤ 1，整数m ≥ 2.设I（j）是（0，p）的互不相交的子区间，1 ≤ j ≤ J，满足H/2 ≤|I（j）|≤ H，以及（y）p表示y在模p下的非负最小剩余.定义I=Uj=1JI（j），并设χ是模p的Dirichlet非主特征.证明了
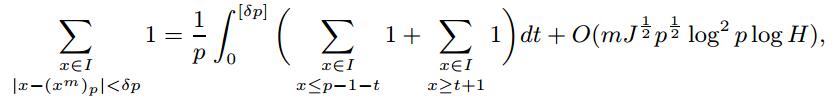
以及
.
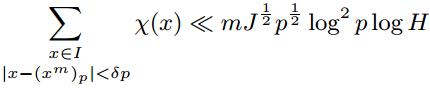设μ=（μi）i ≥ 0为Z+上的测度且p>1，考虑下述离散型p次 Dirichlet型Dp（f）=∑i=0∞μibi（fi-fi+1）（fip-1-fi+1p-1），f ≥ 0，其中 （bi）i ≥ 0 为Z+上的正序列.本文旨在给出空间 Lp（μ）上p次Dirichlet型Dp（f）所对应的第一特征值λ0，p=inf{Dp（f）：‖f‖p=1，f非负且具有紧支撑}的上下界精细估计.
本文在左截断相依数据下，利用局部线性估计的方法，先提出了条件分布函数的双核估计；然后利用该估计导出了条件分位数的双核局部线性估计，并建立了这些估计的渐近正态性结果；最后，通过模拟显示该估计在偏移和边界点调节上要比一般的核估计更好.
本文考虑的是允许采用比例再保险策略和投资策略的两个保险公司如何寻找最优合并时刻的问题. 两个保险公司的风险过程由漂移布朗运动刻画，目标为最大化它们的生存概率. 各个公司的安全负荷系数和波动系数在决定两公司是否要合并时起到了关键作用. 决定合并后，公司合并费用，合并前后公司的生存概率状况在决定最优合并时刻时起到了关键作用. 我们分两种情况讨论了这个问题并分别给出相应情况下的最优策略和值函数.
利用绝对正规范数生成凸函数的关系，给出了加权平均范数空间上Ptolemy常数的取值，解决了一些文献的遗留问题，并在一些具体的空间上给出了Ptolemy常数的新结果.
利用高斯和与次数矩阵Smith标准形的不变因子，给出了有限域上广义对角多项式指数和的估计，从而改进了Deligne——Weil型估计这类多项式指数和的结果.
在许多大型队列研究中，采用节约成本并能提高效率的抽样机制至关重要，基于因变量的抽样设计正是这样一种有偏抽样机制.这种方法最大的优点在于：能够将资源集中在那些包含有更多的协变量与因变量关系信息的研究群体上.本文研究基于因变量抽样设计下的线性模型中回归方程显著性检验以及回归系数显著性检验问题.基于一种半参数经验轮廓似然的方法，我们分别为回归方程检验与回归系数检验提出了相应的检验统计量，获得了所提出检验统计量的渐近性质.通过模拟研究评估了所提出的检验方法在有限样本下的表现，并应用提出的方法分析了一个孕妇分娩的实际数据.
令M1为一个有限的von Neumann代数，τ1为其上的一个忠实正规迹态. 我们将证明，如果M1中存在一列两两正交的酉元列{uk：k∈N}，则对任意具有忠实正规迹态τ2的有限vonNeumann代数 M2 （≠C），迹自由积（M1，τ1） * （M2，τ2） 是Ⅱ1型因子.作为推论可以得出，如果M1有一个von Neumann子代数N不包含最小投影，则对任意具有忠实迹态τ2的有限von Neumann代数M2（≠C），迹自由积（M1，τ1）*（M2，τ2）是Ⅱ1型因子.
本文首先给出复Banach空间单位球上一类α次星形映射齐次展开式各项的精细估计，特别当这些映射又是k折对称映射时，估计还是精确的.其次建立Cn中单位多圆柱上上述推广映射齐次展开式各项的精细估计，同样当这些映射又是k折对称映射时，估计仍是精确的.由此证明了多复变数中关于α次星形映射的弱Bieberbach猜想，且所得到的估计都能回到单复变数的情形.
设p>0，s ≥ 0，q>max{-n-1，-s-1}，本文探讨了单位球上F（p，q，s）空间的一种等价刻画和分解问题.具体结果为：（1） f∈ F（p，q，s）当且仅当f∈ H（B），且Ip=supa∈B∫B|Rα，γf（z）|p（1-|z|2）q+pγ-p（1-|φa（z）|2）sdv（z）<∞，其中α>-1 和γ>max{0，1-（q+s+1）/p，1-（q+n+1）/p}. （2） 若{dk}∈ ∫p，则存在序列{wk}⊂B，使得 f（z）=∑k=1∞（dk（1-|wk|2）t+1）/（1-<z，wk>）t+（q+n+1）/p）（z∈B）属于F（p，q，s），其中t>max{1-1/p，0}（q+n+1）+max{1/p，1}s-1.
本文研究了速度场的旋度与三维磁场微极流方程组光滑解的整体存在性之间的关系，将Constantin与Fefferman关于Navier——Stokes方程组的成果推广到了一个相当完备的不可压缩流体方程组系统，使得相应的结果在微极流方程组以及MHD方程组中都成立.
