回顾了建立KS-代数的研究背景,系统介绍了KS-代数的定义和性质以及超有限KS-代数、非超有限KS-代数、KS-格的构造和强KS-代数的研究结果,同时分析了KS-代数和经典的不变子空间、Kadison可迁代数、von Neumann代数生成元等问题之间的联系;讨论了非自伴代数的运算,给出了两种不同构造非自伴代数的运算法则;在此基础上,提出了未来学科发展有待研究的16个问题.
本文主要考虑如下Kirchhoff问题
![]()
其中a,b是正的常数.我们证明了基态解,即上述问题的极小能量解的存在性.同时,如果假定Q ≡ 1,且h(x)满足一定的条件,可以证明下述问题
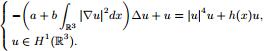
的基态解的存在性.
本文给出一种几何的子轨形群胚的定义,还给出了判定子轨形群胚的依据,并证明了紧子轨形群胚的轨形管状邻域、紧辛子轨形群胚的辛邻域和紧Lagrangian子轨形群胚的Lagrangian邻域的存在性.
本文研究了如下非局部临界指数问题
![]()
其中Ω⊂R4是一个有界光滑区域且0 ∈ Ω,a≥0,b,λ,μ > 0,1 < q < 2,0 < β < 2.利用变分方法,我们获得了一些存在性与多重性结果.
迭代运算下,函数值可以交叉于不同的子区间,使得逐段单调函数的高度异常复杂.本文考虑一个非单调点的连续函数类.首先给出高度的充分必要条件,以此获得此类函数的一种划分.其次针对函数类的一个非空子集,给出判定拓扑共轭的充分必要条件和构造拓扑共轭的新方法.进一步地,我们阐明这样的事实:两个逐段单调函数拓扑共轭是其高度相等的充分不必要条件,最后举例说明.
本文在一般矩条件下研究了同分布的NA随机变量序列和独立同分布的随机变量序列的收敛性,得到了推广形式的Baum-Katz定理和强大数律,这些结果推广了已知的一些文献中相应的结果.
叶德平等人介绍了任意实数p(p≠-n)的多重凸体的Lp-混合几何表面积.本文给出了关于任意实数p(p≠n)的多重星体的Lp-对偶混合几何表面积的概念,并且建立了一些相关不等式.
Lp平移不变子空间中的采样研究通常要求生成函数属于一个不依赖于p的Wiener amalgam空间,此条件因不能控制p而显得太强.本文主要讨论生成函数属于混合范数空间时,非衰减平移不变空间中的非均匀平均采样与重构.生成函数属于混合范数空间的条件弱于Wiener amalgam空间且依赖于参数p.基于混合范数空间中的一些引理,针对两种平均采样泛函建立了采样稳定性,并给出了对应的具有指数收敛的迭代重构算法.
本文利用新的方法给出了4阶正则微分算子耦合自共轭边界条件的基本标准型,新标准型中的4个分块小矩阵为对称矩阵,且其行列式的模为1.这与2阶微分算子耦合边界条件的标准型极为类似,这为给出一般的高阶微分算子自共轭边界条件标准型提供了新的思路.
设TΩ是带粗糙核的Calderón-Zygmund奇异积分算子,I为任意真包含在单位圆周S1上的闭圆弧.本文证明,若Ω支在I上并在I上单调,那么TΩ是从Hardy空间H1(R2)到L1(R2)的有界算子当且仅当||Ω||Llog L(S1) < ∞.
讨论了随机环境中受控分枝过程{Zn:n ∈ N}的极限问题.给出了过程在{Sn:n ∈ N}下的规范化过程{?n:n ∈ N}几乎处处收敛、L1收敛和L2收敛的充分条件,以及过程{?n:n ∈ N}的极限非退化于0的充分条件和必要条件,得到了过程在{In:n ∈ N}下的规范化过程{Wn:n ∈ N}几乎处处收敛和L1收敛的充分条件.
本文研究由分数扩散过程决定的测度(分数扩散测度)的随机分析理论.首先,利用Bismut方法给出拉回公式,得到了分数扩散测度的分部积分公式.进一步,利用此公式,将Wiener测度下的经典的鞅表示定理推广到分数扩散测度下的鞅表示定理.
本文将耦合方法应用于非时齐马氏过程,推广了时齐情形的耦合基本定理,为后续研究非时齐马氏过程的耦合提供了理论基础.
本文给出新Dirichlet级数Σn=0∞aneλns的收敛横坐标σc、一致收敛横坐标σu和绝对收敛横坐标σa的定义.通过指数λn和系数an的关系去估计三个横坐标,并补充证明两类Dirichlet级数Σn=0∞aneλns和Σn=0∞ane-λns的收敛条件是一致的.