设A是Hilbert空间H上的von Neumann代数的CSL子代数.本文证明了,在一定的条件下,A上的Jordan (α,β)-导子是(α,β)-导子,其中α,β是A上的两个自同构.还证明了在没有添加任何条件的情况之下,CSL代数上的任意Jordan (α,β)-导子是(α,β)-导子.另外,讨论了von Neumann代数中的CSL子代数上的n次幂(α,β)-映射.
首先证明了M-矩阵的H-相容分裂都是正则分裂,反之不成立.这表明对于M-矩阵而言,其正则分裂包含H-相容分裂.然后针对系数矩阵为M-矩阵的线性互补问题,建立了两个收敛定理:一是模系多分裂迭代方法关于正则分裂的收敛定理;二是模系二级多分裂迭代方法关于外迭代为正则分裂和内迭代为弱正则分裂的收敛定理.
提出了一种通过置换因子的水平来构造具有较小可卷型L2-偏差的混合水平均匀设计的新方法.首先建立了混合水平设计的平均可卷型L2-偏差与广义字长型的定量关系,并以具有较小广义字长型的混合水平设计为初始设计,对其作水平置换,计算其可卷型L2-偏差,找到具有最小的可卷型L2-偏差的设计就是相对较好的设计.为了使算法更加有效,还运用了可卷型L2-偏差的两个性质.数值结果显示通过这种方法构造的设计在可卷型L2-偏差下表现良好.
对于Rn中一般位置的点构形,定义了第r个极小凸包距离的概念,证明了极小凸包距离和极小点-超平面距离之间的一个最优不等式.该不等式的一个直接推论是:对于Rn中一个k-维单纯复形K,我们能用其顶点集的极小点-超平面距离下估计K的Gromov—— Guth厚度.进一步,在每一个维数k,构造了例子说明该下界几乎是最优的.
研究了典型几何上规范Ricci流下Laplace——Beltrami算子第一特征值的发展行为.在每一个Bianchi类中,我们估计了特征值的导数.构造了Ricci流下的单调量并得到了特征值的上下界估计.
通过量子信道的Kraus算子,提出了对角量子信道的概念,证明了对角量子信道的一些性质:一个量子信道成为对角量子信道的充要条件是所有对角矩阵都是它的不动点;同一对角量子信道的所有压缩矩阵具有相同的秩;一个对角量子信道不可纠错的充要条件是其压缩矩阵是行满秩的.进而证明了一个对角量子信道在整个空间上可纠错当且仅当其压缩矩阵为1秩阵.最后,利用一个具体例子给出了构造对角量子信道的码空间的一种方法.
我们在最大框架下研究定义于单纯形Td⊂Rd的m重积上的Sobolev类逼近问题的易处理性.对于信息类Λall,得到了问题具有几种易处理性相匹配的充要条件,结果是依赖于问题参数的.本文是相应积分问题的继续研究.
研究压缩感知中的块稀疏信号重构问题,主要对混合l2/l1极小化方法建立了一类改进的可重构条件.具体地说,本文证明若测量矩阵满足条件δk+θk,k<1,则混合l2/l1极小化方法可精确重构(无噪声情形)或鲁棒重构(有噪声情形)原始块k-稀疏信号.进而表明本文给出的新条件弱于现有文献所给出的条件.
讨论了二阶常微分方程边值问题
![]()
正解的存在性,其中f:[0,1]×R+→R+连续.给出了该问题存在正解的新特征值判据,该判据改进了以前文献中的相关结果.我们的论证基于锥上的不动点指数理论.
图G=(V,E)的一个混合控制集是一个满足如下条件的集合D⊆V∪E:不在D中的每个点或每条边都相邻或关联于D中的至少一个点或一条边.确定图的最小基数的混合控制集的问题称为混合控制问题.本文研究混合控制问题的算法复杂性,证明了混合控制问题在无向路图上是NP-完全的,但在块图上有线性时间算法.无向路图和块图都是弦图的子类,又是树的母类.
利用Bloch型空间中函数的导数的估计,通过构造一些新的检验函数,运用解析函数的性质与算子理论,给出了不同Bloch型空间中的积型算子紧性的特征.
在一致光滑与2-一致凸Banach空间里,引进一个新的混合投影算法,找到了两族半相对非扩张映射的公共不动点集,有限个一般均衡问题的解集与宽松的协合算子的有限个变分不等式问题解集的公共元.所得结果推广了许多最近成果.
设G是剩余有限minimax可解群,α是G的自同构且φ:G→G(g→[g,α])是满射,则有以下结果:(1)当αp=1时,G是幂零类不超过h(p)的幂零群的有限扩张,其中h(p)是只与p有关的函数; (2)当α4=1时,G存在一个指数有限的特征子群H,使得H"≤Z(H)和CH(α2)是Abel群.并且CG(α2)和G/[G,α2]都是Abel群的有限扩张.
本文考虑,当一个紧辛轨形群胚(X,ω)沿着光滑点作加权涨开时,它的形如〈α1,…,αm,[pt]〉g,AX的轨形Gromov—— Witten不变量的变化公式,其中[pt]∈HdR2n(X)是生成元,dimX=2n.我们证明了对于非零A∈H2(|X|,Z),
〈α1,…,αm,[pt]〉g,AX
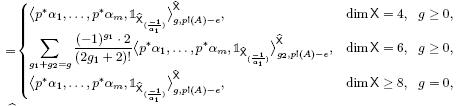
其中![]() 是X沿一光滑点的权a=(a1,…,an)的加权涨开,且a1≥ai,2≤i≤n.
是X沿一光滑点的权a=(a1,…,an)的加权涨开,且a1≥ai,2≤i≤n.
给出非单C*-代数α-比较性的等价刻画:当每个τ∈QT(A⊗K)均为忠实时,A具有α-比较性,当且仅当对于任意的〈a〉,〈b〉∈Cu(A)且〈a〉∝〈b〉,若α·dτ(a)<dτ(b)(∀τ,∈QT(A⊗K)),则〈a〉≤〈b〉在Cu(A)中成立;一般地,当QT(A⊗K)≠0时,A具有α-比较性,当且仅当对于任意的〈a〉,〈b〉∈Cu(A),若存在η>0,使得dτ(a)≤(α-1-η)dτ(b)(∀τ,∈QT(A⊗K)),则〈a〉≤〈b〉在Cu(A)中成立.